星露谷物语玛鲁数学题答案是什么,游戏中玛鲁是虚幻研究小发明的npc,她有很多关于知识的问题,其中有一个数学问题是比较难的,有玩家不知道具体的答案,接下来小编为大家带来了详细介绍。

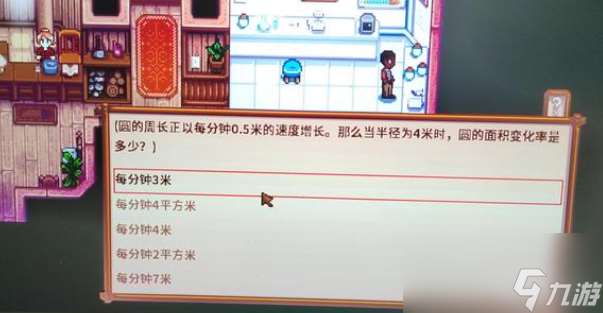
问题:圆的周长正以每分钟0.5米的速度增长。那么当半径为4米时,圆的面积变化率是多少?
答案:每分钟2平方米
以下是解题过程:
圆的周长 \( C \) 与半径 \( r \) 的关系为:\[lbk] C = 2\pi r \[rbk]根据题意,圆的周长正以每分钟0.5米的速度增长,即:\[lbk] \frac{dC}{dt} = 0.5 \text{ m/min} \[rbk]我们需要求的是当半径 \( r \) 为4米时,圆的面积变化率。
圆的面积 \( A \) 与半径 \( r \) 的关系为:\[lbk] A = \pi r^2 \[rbk]首先,我们需要找到面积变化率 \(\frac{dA}{dt}\)。
运用链式法则,我们可以写成:\[lbk] \frac{dA}{dt} = \frac{dA}{dr} \cdot \frac{dr}{dt} \[rbk]已知:\[lbk] A = \pi r^2 \[rbk]对 \( r \) 求导:\[lbk] \frac{dA}{dr} = 2\pi r \[rbk]接下来,我们需要求出 \(\frac{dr}{dt}\)。
已知:\[lbk] C = 2\pi r \[rbk]对时间 \( t \) 求导:\[lbk] \frac{dC}{dt} = 2\pi \frac{dr}{dt} \[rbk]将 \(\frac{dC}{dt} = 0.5 \) 代入上式:\[lbk] 0.5 = 2\pi \frac{dr}{dt} \[rbk]解得:\[lbk] \frac{dr}{dt} = \frac{0.5}{2\pi} = \frac{1}{4\pi} \text{ m/min} \[rbk]
现在我们有:\[lbk] \frac{dA}{dt} = 2\pi r \cdot \frac{1}{4\pi} = \frac{r}{2} \[rbk]当半径 \( r = 4 \) 米时:\[lbk] \frac{dA}{dt} = \frac{4}{2} = 2 \text{ m}^2/\text{min} \[rbk]
因此,当半径为4米时,圆的面积变化率是 \( 2 \text{ m}^2/\text{min} \)。当半径为4米时,圆的面积变化率是每分钟2平方米。因此,答案是:当半径为4米时,圆的面积变化率是 2平方米每分钟。


















